INTRODUCING SYSTEM DYNAMICS INTO THE TRADITIONAL SECONDARY CURRICULUM: THE CC-STADUS PROJECT'S SEARCH FOR LEVERAGE POINTS

Ron Zaraza, Wilson HS, 1151 SW Vermont, Portland OR 97219, USA

Diana Fisher, Franklin HS, 5405 SE Woodward, Portland OR USA

Teachers are among the most “conservative” professionals. While they may be extremely creative in their classrooms, and tremendous risk-takers in the way they work with students, they remain staunchly conservative and protective of their subject matter. Tradition has defined what the appropriate content is in a Global Studies class, a Literature class, or an Algebra class. Any changes in instruction that threaten a teacher’s ability to present the great bulk of material they feel they must cover will be met with resistance. Every change in education is met by the question “How can I

add . . . when I’m already having a hard time covering the syllabus?”

Attempts to bring systems thinking and system dynamics into the K-12 classroom have faced the same problem. Teachers are pressed for time and skeptical about changes that may appear to add new topics to an already full curriculum. When such new ideas are outside their own professional content expertise, they are nervous about their own mastery of the material as well. Traditionally, educational innovations have emphasized positive change in outcomes: Students will learn better/faster/more. Yet most educational innovations, even though less “foreign” than the introduction of systems concepts, are only slowly and often incompletely implemented. Better/faster/more simply isn’t enough to insure acceptance. Successful integration of systems concepts into the curriculum will suffer a similar fate unless the unique capabilities of systems work can be made obvious. While systems thinking and dynamics can help students learn content better/faster/more, the truly impressive advantage of systems work is the way it allows students to ask better and more important questions. That results in learning through “conversations”, through thoughtful involvement of students. The opportunity to experience such learning is a powerful force in convincing teachers to begin to use systems. However, the initial entry into the use of systems remains a stumbling block.

During the four years the CC–STADUS (Cross-Curricular Systems Thinking and Dynamics Using STELLA) Project has trained teachers in the development of models and curriculum for K-12 classroom use, the more than 160 participants have gained a wealth of experience in how system dynamics can be introduced to students in both single discipline and cross-curricular environments. It has become clear that single-subject use is the easiest way to introduce systems ideas to both teachers and students. Further, it is clear that there are certain natural "entry points" into the traditional courses.

Each subject includes topics that are natural systems topics. Those topics constitute leverage points, topics that clearly show the potential of dynamic modeling. Introduction of dynamic models at those points opens up both the discipline and system dynamics for student inquiry. The advantages of dynamic models in addressing the topics are dramatic and obvious. Thus, those topics should be emphasized in training of teachers as they begin to use system dynamics. The power of these basic models presents a compelling argument for the introduction of systems into courses. Too often complex and detailed models are presented to novices as an example of the power of dynamic modeling to build knowledge. Those complex models are often intimidating and tend to obscure the real power of dynamic modeling: even simple models can have a major impact on student learning. These simple but powerful models provide the real leverage that can attract teachers to modeling.

Within the sciences, each field has distinct topics that can be used to introduce system dynamics. Two approaches are being used by CC–STADUS teachers in physics. The first focuses on the basic mathematical definitions of the concepts of motion. Physics has often been referred to as “the study of rates”. The language used to describe flows in systems is identical to that used in defining basic concepts of motion. The ideas of position, rate of change of position (velocity), and rate of change of velocity (acceleration) can be easily developed through simple models. These models provide exposure to two of the four basic model structures, linear and quadratic, that CC–STADUS training focuses on.

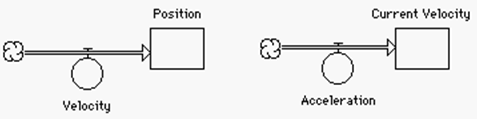
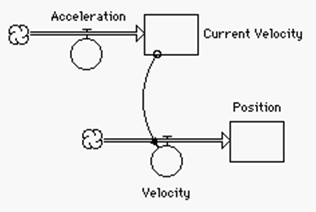
These basic linear structures are among the first taught to teachers in the CC–STADUS training. The linear change in position when velocity is constant and the linear change in velocity when acceleration is constant are also among the most basic concepts of motion taught in physics. These models illustrate the ideas in a very simple way, reinforcing the physics and math. Dealing with position change for an accelerated object is conceptually more difficult. The fact that the distance is no longer a linear function of time is not easily understood by students. The model shown on the next page, however, illustrates the reality of the situation. The acceleration constantly changes the velocity which, in turn, constantly changes the rate at which position changes, The model structure makes obvious what the algebra does not. Dynamic models such as these provide a visual reinforcement of the concepts normally introduced algebraically. The structures explain the relationships of the variables. These models may then be expanded to deal with all the other basic concepts of motion.

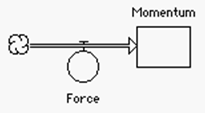
The alternative physics approach utilizes models illustrating the concepts of impulse, momentum, and the conservation laws. Effectively, these models introduce physics through Newton’s laws of motion.. The emphasis is less on developing models that are analogues of mathematical relationships and more on physical concepts. This allows an alternative approach to developing physics in secondary schools, one usually restricted to college students with advanced mathematical training. The two models shown below are examples of these basic models. Once again the starting model structures are linear.

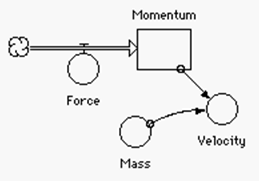
Grant participants have developed a broad physics curriculum around both types of models. The graphical representation of concepts provides an alternative approach to developing an understanding of basic physics. That, however, does not provide a compelling reason for using models in physics. Teachers already have several ways of presenting these physics concepts. One more way, even if very versatile, seems unnecessary. The use of models is only compelling if the models give students and teachers capabilities the traditional methods do not. These simple models do provide a good base for models that deal with real problems of interest to students. These problems are not normally addressed because they cannot be solved using the traditional mathematical tools at the students’ disposal. Non-constant accelerations (their car!), motion with air resistance (sky diving), and non–constant mass problems (the flight of a rocket) are all problems that students ask about. The ability to discuss these and similar problems provides the motivation or leverage which convinces teachers to bring systems into physics.

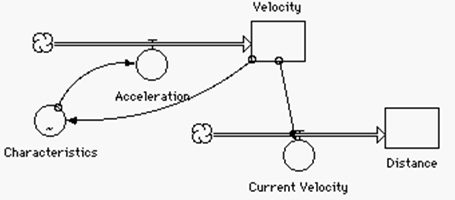
The simple addition of a graphical converter which makes acceleration dependent on current velocity turns the basic quadratic model used to describe accelerated motion into one that can describe the behavior of cars and other objects that have non-constant accelerations. Students can use popular magazines such as Car and Driver or Road and Track as physics reference materials, calculating acceleration graphs for various cars. They can even drag race cars against each other.

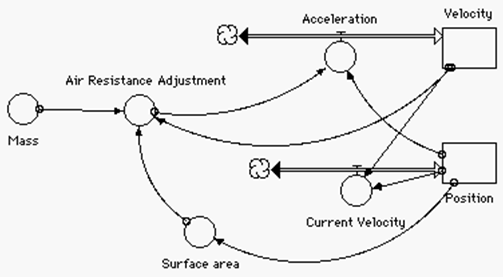
The same basic model can be modified to deal with air resistance. This is a problem that frustrates many physics students. They grow weary of problems that always require them to ignore friction, air resistance, and other factors that are part of real life. Only one secondary text, PSSC Physics , deals with friction. The approach is confusing, and beyond the reach of most students. This model allows students to explore the work in that text, as well as other problems. In particular, the behavior of a sky diver as she falls freely, reaches terminal velocity, pulls her ‘chute and slows to a new terminal velocity can be studied. More importantly, the differences that changing body orientation (fetal position, spread–eagle, head down) can not only be talked about conceptually, but numerically, an impossibility without modeling.

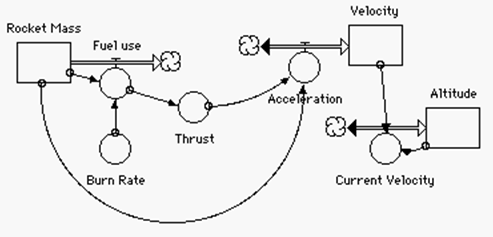
Force/Impulse/Momentum problems are dealt with extensively in physics. Yet the most interesting can only be approached conceptually: the flight of a rocket. The algebraic equations taught at the secondary level do not allow mass and velocity changes to be dealt with simultaneously. Again, the quadratic modeling structure can be easily adapted, as seen above. This model can even be modified to use actual thrust data for commercially available model rocket engines, allowing students to compare experimental and theoretical performance. Once these mechanics/kinematics models have been used, expansion to electricity, magnetism, and radioactive decay becomes obvious and simple.

Biology presents its own obvious starting points. Regardless of the course emphasis, almost all secondary biology courses deal with population growth and ecology. Both are excellent leverage points. Traditional study of these topics has been qualitative. Dynamic models provide a way to include quantitative work as well. The study of the reproduction of micro-organisms allows the introduction of the concept of exponential growth. Simple exponential growth models allow students to explore a wealth of problems discussed in biology. As their experience grows, students or teachers add complexity, placing different controlling factors in the model. They may also link models that affect each other. This opens up the possibility of exploring ecosystems. Using simple models focusing on a single organism and its food supply (an herbivore and the plants it eats) or a simple predator–prey model (wolf-moose), students can explore the relationship by changing rates, variables, and population sizes. Ultimately students begin to understand the concept of a biological system from experimentation with models.

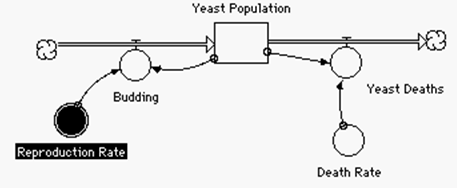
The simple population model shown above is a classic starting point for modeling in biology classes. In this case, it was developed after students had done a long term experiment with yeast growth. The model was built to reflect actual data. Of course, it is greatly simplified, allowing unrestricted growth. The real learning begins as students attempt to explain why such growth cannot happen, and what patterns should occur. The option of exploring these ideas numerically is the “hook” that often catches teachers. The model below shows a simple modification to the model, an adjustment in reproduction and deaths due to depletion of nutrients.

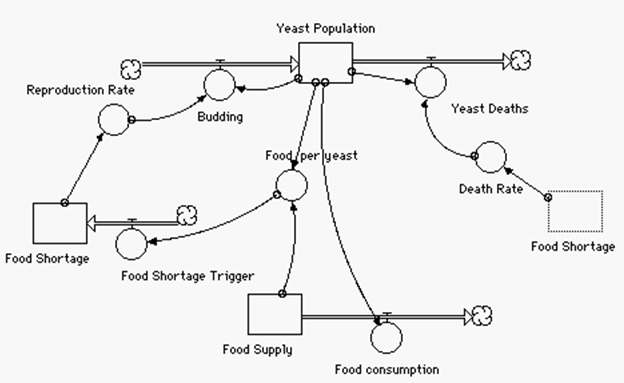
The model can be extended further to look at the effects of waste. This ability to “grow” a model as student interests, abilities, and questions dictate further enhances the attractiveness of modeling.

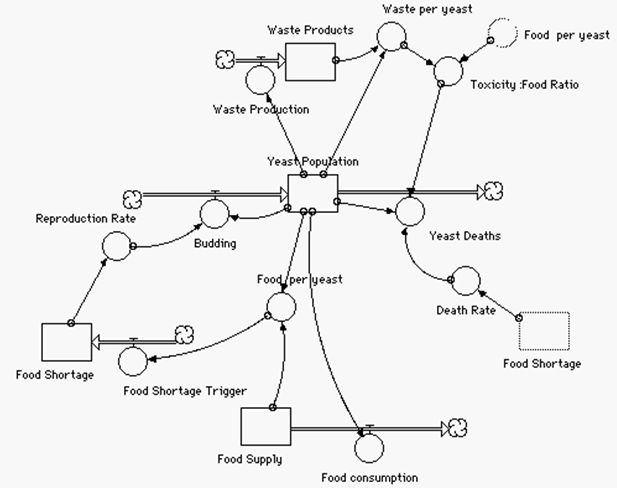
It is the quantitative nature of this work, as well as the opportunity to experiment, that provides the motivation for biology teachers to begin using models. Discussion of exponential growth is compelling when graphs and tables can be easily generated. The structure of an exponential growth model provides insight to the process, facilitating understanding. The reality that there are limits to growth can be easily seen working with models. Understanding why and how those limits apply can be explored with models. They move discussions from the “hand–waving” to the real, because the variables can be manipulated. As the models are expanded and linked, students can truly explore and experiment with the interactions of an ecosystem, something simply not possible without dynamic modeling. For many biology teachers, that capability alone provides sufficient motivation to begin using systems in their classes.

Chemistry has presented more of a problem. The field seems ideally suited for dynamic models, with the same emphasis on rates seen in physics. However, successful models have been few. While some models have been attempted, most are either too complex for easy student use or too narrow in their focus. For some models, particularly reaction rate models, accurate data is virtually unobtainable. The only models that have seen substantial use have been heat flow models. While thermodynamics is certainly an important part of chemistry, thermodynamics models are not strong motivators, do not provide the leverage needed to broadly attract chemistry teachers. The true leverage point in this discipline would almost certainly be accurate, easily understood reaction rate and equilibrium models. Until such models become available, use in chemistry will remain limited.

The Social Sciences are an area where a large amount of successful work has been done using dynamic models. Introductory work is often based on the same type of exponential growth/population models used in Biology. Often focused on comparisons between industrial and third-world nations, these basic models dramatically present information. Many teachers have become interested in using models in their classes simply through exposure to these models. These low-complexity models provide all the leverage needed to motivate use. These simple models provide a basis for discussion that can evolve into very detailed and sophisticated concepts, even with no further modeling. When the initial systems can be changed to include linked systems and the many modifiers on systems, including impact of disease, wars, emigration and immigration, a depth of understanding of the system can be developed that goes far beyond traditional classroom experience. The possibility of such work, based on simple models, makes social science teachers eager to use models.

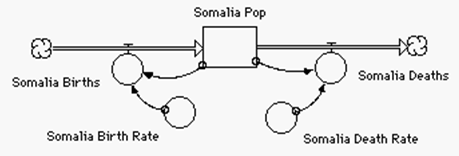
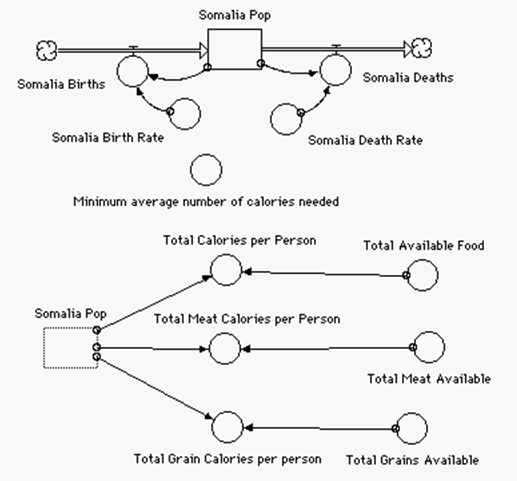
The sequence of models shown here illustrates how even small additions to models can broaden the scope of discussion in social science classes. The first model is the familiar population model also used in biology. In this case, it was being used to explore the present and future population problems of third–world nations. The basic model, run for 100 years, tells a dramatic story. To emphasize this, two population models are combined and displayed on the same graph and tables, showing the difference between population growth in an industrialized nation and a third–world nation. Student responses to this model direct the next step. One option is the addition of two converters to the basic population model. This allows changes in land availability to be explored, an even more dramatic development.

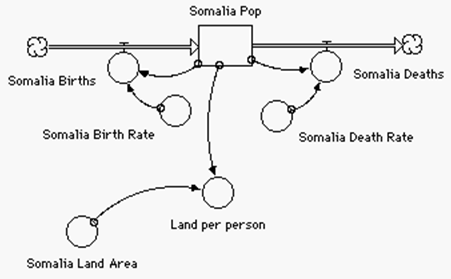
Similar modifications allow food availability to be explored as well. The result of all these models is a wealth of information about the problems faced by third–world nations. It is a powerful starting point for discussion. In some cases the discussion leads to further models. In others, the extensions are explored without additional models.

Like physics, much work in mathematics focuses on rates. Concepts from slope through the second derivative can be easily described by the rates used in systems models. An entry point for models in mathematics is the use of a motion detector in conjunction with dynamic models of motion. The motion detector can be used to produce a graphical and a conceptual view of functions from their rates of change. A model can be introduced to generate the same patterns. The structure of the model gives clues to the pattern’s causes. The models then allow students to explore problems and applications that involve the functions. This allows students to use a conceptual perspective, rather than the traditional methods.

This process can be repeated wherever problems are presented in which the independent variable is time. Thus, each new topic becomes a potential leverage point where models can be used to address the topic conceptually before, or in parallel with more traditional treatments. The problems can be modeled, expanded, and explained by the students, significantly enhancing their experiences and demonstrating the relevance of mathematical study to other disciplines.

Perhaps the most unusual work done by the CC–STADUS project has been the work done in literature by Tim Joy and a few others. The whole idea of using systems in literature seems odd to some. However, the plot of a book is essentially an interplay among characters, in short, a system of interactions. One of the things literature teachers want students to do is analyze and understand those interactions and the motivations behind them. They want students to write about them, and discuss them. The discussion part is the difficult piece. Usually only a few students are truly engaged. Dynamic models can provide a structure for generating those discussions and involving more students.

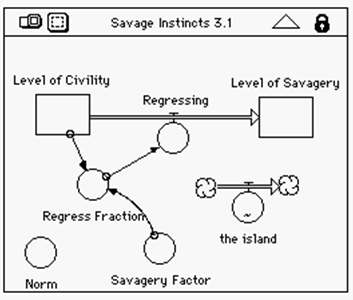
Using very simple models, like the one shown above, Tim has pioneered work in which students trace character development through changes in specific traits. Using the authoring level of a STELLA model, students are presented with a succession of events and quotations from the book. Students are asked to adjust the change in the level of the trait before the model resumes. This adjustment is accompanied by written justification based on passages in the text. 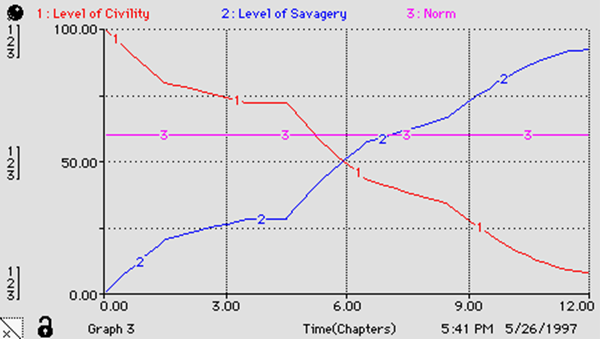In the course of running the complete model students generate a graph of the character’s behavior. These graphs, like the one shown on the next page, are displayed in class. Students then are asked to explain or justify their interpretations as displayed in their graphs. The result is an animated, sometimes passionate discussion. The potential for that level of student involvement serves as a strong motivator for Literature teachers. It provides enough leverage to involve teachers. Additionally, the “Savage Instincts/Lord of the Flies” models introduce students to the use of systems at a level that is accessible to virtually everyone. Discussion and further student modeling bring students more fully into the understanding of dynamic systems.

The use of system dynamics in the K-12 environment, and particularly at the secondary level, is growing at an impressive rate. Advocates compare it to an infection, with the exponential growth only now in the toe of the curve. If the “infection” is to grow, if it is not to level off, modeling advocates must emphasize the leverage points as they recruit other users.

References

Forrester, J. W. 1971. Principles of Systems. Portland, OR: Productivity Press.

Kauffman, D. L., Jr. 1980. Systems 1: An Introduction to Systems Thinking. Cambridge, Mass: Pegasus Communications.

Meadows, D. H., D. L. Meadows, and J. Randers. 1992 Beyond the Limits. Cambridge, Mass: Pegasus Communications.

Meadows, D. H. 1991. The Global Citizen. Cambridge, Mass: Pegasus Communications.

Richmond, B., and S. Peterson. 1993 STELLA II An Introduction to Systems Thinking. High Performance Systems, 45 Lyme Road, Hanover, NH 03755, USA.

______. 1993. STELLA II Applications. High Performance Systems, 45 Lyme Road, Hanover, NH 03755, USA.

Richmond, B. 1994. Authoring Module. High Performance Systems, 45 Lyme Road, Hanover, NH 03755, USA.

Roberts, N., D. Anderson, R. Deal, M. Garet, and W. Shaffer. 1983. Introduction to Computer Simulation: A System Dynamics Modeling Approach. Portland, OR: Productivity Press.

Senge, P. M. 1990. The Fifth Discipline. New York: Doubleday.