Systems Dynamics in the Fisheries of Northeast Arctic Cod

Harald Yndestad

Aalesund College

Fogd Grevesveg 9, 6009 Aalesund, Norway

Abstract

Northeast Arctic cod is one of the largest stocks of cod in the world. The cod biomass is influenced by temperature cycles related to the earth nutation. A stationary dynamic cycle is estimated in the recruitment and causes a dynamic instability between the biomass and the quota of landings. The deterministic property of the cycle opens a new perspective on forecasting biological economical resources in the Barents Sea.

Keywords

Northeast Arctic cod; Earth nutation; Stationary cycles; Forecasting;

1 Introduction

Northeast Arctic cod is one of the largest stocks of cod in the world. During centuries this stock of cod has been of utmost importance to the economic growth of western Norway. People living by fishing have always known that the stock of cod has dynamic properties. Some years the influx of cod is abundant and some years the influx may be insufficient in relation to the demand. Better forecasting over a time span of 5-10 years, will be crucial for better planning of an economical and sustainable utilisation of the cod biomass.

In 1994 it was found that the time series related to the quantities of North Atlantic cod has a 6-7 year cycle in the Fourier spectrum amplitude. The question then was: Is this a stationary cycle? If so, there is a possibility of a more precise prediction of ecology resources and hence a proper basis for fishery investments. Further research revealed the cycle in the fry abundance and even in the cod quotas. The same cycle was found in the temperature of the Barents Sea and a relation was found between this temperature cycle and the earth nutation, as the cause of causes (Yndestad, 1994c).

This paper focuses on some methodical aspects of system dynamics of the Northeast Arctic stock of cod related to a general system theory.

2 System theory

A system is a set of social, biological, ecological, technological or material partners co-operating for a common purpose. A doctrine of a general system theory (Yndestad, 1996a) may be formulated by the dual views

System = System ontology + System Epistemology

System ontology = System Architecture + System Dynamics

System Epistemology = System Ethic + System Learning

A general dynamic system S(t) may be expressed by a set of partners P(t) related by the binding A(t).

S(t) = {A(t),{p₁(t), p₂(t),,, p_n(t)}, n = f(t)} Î w

Where w is the common purpose and n is the number of partners at the time t. In this case the purpose is a sustainable biomass. The partners in the system are the earth system, the temperature system in the Barents Sea, the ecological system in the Barents Sea, the cod biomass system in the Barents Sea, the cod landings system and the cod market system. The binding A(t) is the relation between the partners. This theory implicates that systems are non-linear and structural unstable by nature. When the state of one partner is changed, it will affect all other partners. Systems are recursively made of subsystems

S_i(t) = {A_i-1(t), S_i-1(t)} Î w

Where i is the abstraction level i = {0,1, 2,,}. This implicates that systems are made of systems at lower abstraction levels. In this case all systems from the market system to the planetary system have subsystems. A consequence of this theory is that system dynamics on one level will influence the state of all partners in the system. This property explains why time series measured in systems has a Wiener spectre where the amplitude is falling by 1/frequency. There is no theory for how to predict dynamics in such a complex system. Even if we had online access to all the states in the system, it would be extremely difficult to forecast 5 to 10 years ahead in time.

System epistemology is the dual view of system ontology that represents a non-deterministic view of the reality. Where system ethics is the aim a system is striving fore. System learning is the strategy, which a system chooses to reach the aim. Through this doctrine, system is something more than a sum of interacting parts. Systems are a dynamic process where the dynamics is a synthesis of the system architecture, systems ethics and a free will of learning. This theory implies that systems have knowledge to adapt to the dynamics of its partners. In this case it means that the ecological systems in the Barents Sea have learned how to take advantage of the stationary dynamics. The market system and the landing system are adapting to the system dynamics by learning more about the ecological system.

The cycle theory

The theory in this paper is based that system has a stationary cycle of 18.6 years related to the earth nutation. According to the general system theory, a dynamic change in one partner will influence the state of all others. In this case the earth nutation represents a dominant energy compared to the other partners in the system. The other partners are the temperature balances in the Barents Sea, the ecological system in the Barents Sea, the cod biomass system, the landing system and the market system. The earth nutation represents a small cyclic change on the earth rotation, but since the other partners have much less energy, they will in the long run learn how to adopt to the stationary dynamics related to the earth nutation.

3 System identification

According to the general system theory, systems have mutual influence on common partners.

Earth dynamics

The earth dynamics is influenced by the dynamics of the planetary system. The most important earth dynamics p_e(t) has the relation

p_e(t) = f(w_dt, w_yt, w_nt, w_pt)

Where t is the time, w_d represents the angle frequency of the earth axis rotation, w_y the earth rotation around the sun, w_n the 18.6 years earth axis nutation and w_p the earth precession of 25800 years. Each of these cycles will influence the dynamics of all the other partners in the system. The effect of the cycles w_y and w_n are well known. In this paper we will discuss the relation to the earth nutation cycle w_n.

Temperature dynamics

In the Barents Sea the warm Golf stream from the south meets a cold stream from north. Russian scientists have measured the temperature in the Barents Sea each month since 1900 (Bochkov, 1982). The mean temperature shows changes between 2.7 and 5.0 degrees Celsius over the last hundred years. In this data series three cycles related to the earth nutation has been estimated (Yndestad, 1996b). The estimated cycles are

Where T is a sampling interval of one year and n is the number of years since the reference year 1900. The mean temperature A₀ = 3.9 and the cycle amplitudes A₁ = 0.4, A₂ = 0.6, A₃ = A₄ = 0.4 degree Celsius. The angle frequency w₁ = 3*w_n = 55.8 years, w₂ = w_n, = 18.6 years and w₃ = w_n/3 = 6.2 years. The phase delay from the reference year 1900 is estimated to be j₁ = 12/12, j₂ = 9.6/12 and j₃ = 336/12 years. The random noise v(nT) has an unknown source. Since the cycles are correlated to the 18.6 years earth nutation, the cycles are stationary and deterministic. The signal/noise - relation is estimated to be about 1.

Biomass dynamics

The biomass of North Arctic cod has changed between 750.000 tons and 4250.000 tons the last fifty years. This biomass dynamics is modulated by the difference equation

Where the X(nT)-vector represents biomass of each age class, A(nT) is a (n x m) matrix that represents the recruitment, the growth rate and the mortality rate at each age class, U(nT) is the biomass of landings and B(nT) is a (m x m) matrix that distributes the landing on each year class. The recruitment and dynamics of cod is dependent on the dynamics of the food chain in the Barents Sea. Since the food chain in the Barents Sea is temperature dependent, it will adapt to a stationary temperature cycle. This means there is a binding between the temperature cycle and the dynamics of Northeast Arctic cod. These relation is estimated to be (Yndestad, 1996c)

Where x₈₊₍nT) is the spawn biomass, x_n1(nT) is number of one year recruited cod, p_m is the mean production rate (number of one year cod/spawn biomass) and U_RT(nT) represents the dynamic binding between the recruitment and the temperature in the Barents Sea. The dynamic binding to the temperature cycle is estimated to be

This indicates that the recruitment of Northeast Arctic cod is exponentially related to the 18.6/3 = 6.2 years temperature cycle. This means that if the biomass is known, future dynamics in cod recruitment can be estimated.

The dynamics of biomass growth may be computed by the growth rate. The growth rate of Northeast Arctic cod has the relation

Where x_i(nT) is the biomass at the age i, nT is the time and a_i is the growth rate at the age i. This growth rate is expected to be influenced by the sum of three stationary temperature cycles plus a random disturbance from an unknown source. This may be expressed as

Where v(nT) is a temperature disturbance from an unknown source and a_n represents the binding to this source. In this case the estimated mean growth rate for each year class is a₀₀ = 3.33, a₁₀ = 2.10, a₂₀ = 1.95, a₃₀ = 1.61, a₄₀ = 1.55, a₅₀ = 1.47, a₆₀ = 1.35, a₇₀ = 1.26. The temperature dependent growth rate for each year class is estimated to be a₀₁ = 4.00, a₁₁ = 2.25, a₂₁ = 2.33, a₃₁ = 1.71, a₄₁ = 1.56, a₅₁ = 1.43, a₆₁ = 1.35. a₇₁ = 1.26. This indicates that the 6.2 years related growth cycle has approximately the same amplitude the mean growth rate.

Landing dynamics

Biomass

collapse

Rate

R

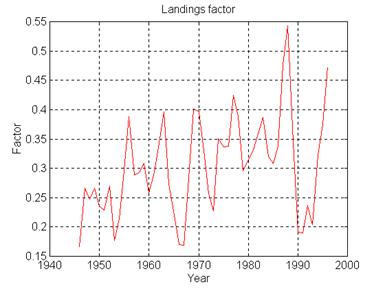
Figure 1 Landing rate from the year 1946 to 1997

The quota of Northeast Arctic cod has changed between 212.000 tons and 1.340.000 tons the last 50 years. This quota is influenced by biomass level, the capacity of the landing system, the dynamics in the market system and the political decision system. Thus the marked system, the landing system and the cod biomass system is a part of a value chain system where each subsystem will influence the dynamics of the other. A landing rate is a policy index that indicates the regulation of biomass landed for distribution to the market. This landing rate may be defined as

Where x₃₊₍nT) is the cod biomass and j_d is a quota decision phase delay. For years there has been a decision phase delay j_d. Recruitment and the growth are heavy influenced by the 6.2 years temperature cycle. Bio dynamics and decision delay thus introduces a positive feedback or instability in the biomass. The landing rate since 1946 is shown on figure 1. The figure shows a typical pattern of an unstable regulation of the cod-landing quota. Periodical cycles of landing rate, a biomass collapse in 1987 and a warning of a new biomass collapse in 1997. This instability is a serious problem for the biomass of Northeast Arctic cod and the fishing industry in Norway. The landing rate controls the biomass of cod. When introducing the landing rate, in the biomass model, we get the autonomous dynamic system

In this case we have a-priori information on expected recruitment and growth related to deterministic temperature cycles. A feed forward strategy and a feedback strategy may then control the system dynamics of Northeast Arctic cod. The feed forward strategy will take care of dynamics related to temperature dependent growth and a feedback strategy will take care of dynamics in mortality.

4 Discussion

Time series of system dynamics in nature usually have a Wiener spectre (1/frequency) amplitude. In this case we have something different. The stationary temperature cycle influence seems to influence the ecological and the economical system of Northeast Arctic cod. A modulated third harmonic temperature cycle of 6.2 year influences the recruitment and the stability of quota regulation of landing. The 18.6 year cycle and the 3*18.6 = 55.8 year cycle influence the maximum biomass level. If the temperature cycle theory is confirmed by hydrographic mesuarment, it will a give a new perspective to the understanding of the ecology dynamics in the Barents Sea and the optimisation of fishery resources.

5 Biography

In 1978 Harald Yndestad received a degree in cybernetics at University of Trondheim. For 10 years he made research on complex IT systems at NDRE in Norway and has since 1982 been ass. professor at Aalesund College. The last years he has been engaged in research on general system theory and system dynamics of Northeast Arctic cod.

6 References

Bochkov, Y.A: (1982) Water temperature in the 0-200 m layer in the Kola-Meridian in the Barents Sea, 1900-1981. Sb. Nauchn. Trud. PINRO, Murmansk, 46: 113-122 (in Russian).

ICES: (1995) Report of the arctic fisheries working group. ICES Headquarters. Copenhagen. Denmark.

Loeng, Ottersen, m.f: (1994) Statistical Modelling of Temperature Variability in the Barents Sea. ICES C.M. 1994. Havforskningsinstituttet i Bergen. Norway.

Yndestad, H: (1996a) A General System Theory. Aalesund College. Norway.

Yndestad, H: (1996b) Stationary Temperature Cycles in the Barents Sea. The cause of causes. The 84'th international ICES Annual Science Conference. Hydrography Committee. Iceland.

Yndestad, H: (1996c) Systems Dynamics of North Arctic Cod. The 84'th international ICES Annual Science Conference. Hydrography Committee. Iceland.