Previous researches have shown that dominant loop analysis is helpful in analyzing the relationships between dynamic system behaviors and close loop structure. Before applying dominant loop analysis methodology, we have to understand the basic loop behaviors. This research first clarified the basic loop behaviors by developing the perspective of implicit loops. Then we concentrated on some basic concepts in using dominant loop analysis, such as the meaning of system behavior and the conditions of dominant loop shift. Using the concepts clarified and developed earlier, we tried to give an explanation of the different analysis results by two different dominant loop analysis approaches developed by Kim and by Richardson. In summary, we hope to enhance the theory basis of System Dynamics by clarifying the basic concepts of system structures and system behaviors.

1. Introduction
The philosophy of System Dynamics lies on the endogenous point of view treating system behavior as generated by the close feedback loop structures. Feedback loops have been regarded as the key point to understand complex systems. Accordingly, the basic behaviors of element loop structures and the interrelations of multiple feedback loops are the main concerns of system dynamics researches. However, as to the behaviors of basic loops, scholars have not thoroughly accepted that one single positive loop generates the exponential growth or decay behavior and a negative loop generates the goal seeking behavior. There are some anomalous examples that leave some unsolved confusions to scholars(Graham, 1973;Richardson, 1995). In analyzing the relationships between system behaviors and loop structures, although many studies have provided valuable methodologies on the dominant loop analysis(Richardson, 1995;Kim, 1995), some basic concepts of dominant loop shift have not been well-defined, such as the conditions of dominant loop shift. Perspective of implicit loops is proposed to explain the confusions about basic loop behaviors, and the "nonlinearity" of feedback loops under which dominant loops may shift is discussed to enhance our understanding about dominant loop analysis. Finally, we applied two dominant loop analysis approaches developed by Richardson and by Kim to illustrate the concepts clarified in this paper.

2. Basic Loop Behavior and the Perspective of implicit loop
To system dynamists, it is well known that a positive loop generates exponential growth or decay and a negative loop corresponds to a goal seeking behavior(Forrester, 1968). Researchers found that this traditionally accepted rule may not always work well. Graham described that in certain conditions positive loop may generate oscillation patterns(Graham, 1973) , and Richardson suggested that a single negative loop may also create oscillation(Richardson, 1995). There seems to be some controversies on the basic loop structure behaviors. As to these controversies, Richardson proposed the concept of implicit loops or pathways to explain how changes in the behavior of a variable of the system occur over time(Richardson, 1995). To extend the concept of implicit loops, this research suggested that the presentation of structure diagrams is the primary reason contributing to confusion about the basic loop behaviors.

In modeling, researchers use flow diagrams as their tool to represent the structures of systems. Whatever computer applications people may use, the common characteristics of these applications are that they all offer the function of bi-flow rates and they all allow the levels to be negative. These two properties structure diagrams together contribute to the implicit loops which might confuse people with the behaviors of pure positive loops and pure negative loops. To illustrate, figure 1 is the structure diagram which scholars have controversies on the positive loop behavior(Graham, 1973) and figure 2 is the simulation result.

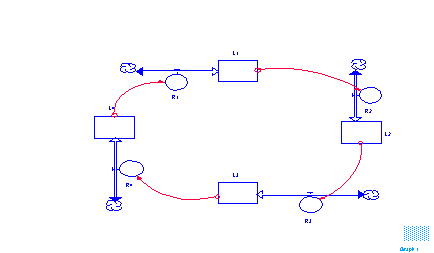
Figure 1 Illustration of Implicit Loop (source:Graham,A.K.

"Priciples on the Relationship Between Structures and Behavior of Dynamics Systems", Ph.D. Dissertation, M.I.T., Cambridge, 1973.)

Figure 2 Behavior of Figure 1


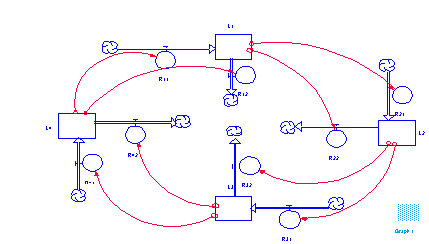
Figure 3 Implicit loop of Figure 1

From the result, we can see obviously that there is only 1 positive loop. With the bi-flow rates and negative levels, figure 1 can be expressed in such a way like figure 3, which contains 8 positive loops and 8 negative loops. These implicit loops come from different combinations of negative or positive levels and inflow or outflow rates.

The concept of implicit loops is very simple. But it gives us some information in model building. First, it articulates the basic loop behavior that is the theory foundation of system dynamics. Second, it reminds us that some problems may occur when modeling. The purpose of model building is to find out the problem structure. The model structure has to be as similar to the real world as possible. Bi-direction flows may be the actual property of some real world case. No matter what kind of presentation model builder may choose, he or she has to be cautious with the gap between the real world and the model presentation. The controversies about basic loop behaviors and the existence of implicit loop are just examples of the gap occurred when modeling.

3. Concepts of Dominant Loop Shift
Prior researches have focused on different approaches to characterize behavior and to define principal structure. Nonlinear systems can endogenously generate bifurcation and chaotic behaviors. However, nonlinear may not be a necessary condition for dominant loop shift. To discuss whether nonolinearity is the necessary condition for dominant loop shift of system behaviors, we first clarify what system behavior means and then we examine what the role nonlinearity plays in dominant loop shift.

When referring to system behavior, one shall mean a particular pattern at a specific time period of the concerned variable. The key concept here is that system behavior is attached with one variable, not the intangible overall system behavior. The behavior of a system is observable only through the patterns of its components, such as levels, rates, or other variables. With different variables, the so called system behavior should be different and the dominant loop of each pattern at each time period should not be all the same.

In system dynamics, nonlinearity often means high order differential equations to be nonlinear. In this sense, some researchers suggest that nonlinearity is the necessary condition for dominant loop shift. However we found that under some circumstances, linearity differential equations may also have dominant loop shift. To have the necessary condition for dominant loop shift, the term nonlinearity should mean the relationship between one level and its net rate. Only when the relationship between the level and its net rate to be nonlinear should the dominant loop shift occur.

Up to now, we have concentrated on the basic concepts in system dynamics and in dominant loop shift. Next, we shall apply these concepts in explaining the result of two dominant loop analysis approaches.

4. Comparison of Two Dominant Loop Analysis Approaches
The two dominant loop analysis approaches we illustrate here are proposed by Richardson and by Kim(Richardson, 1995;Kim, 1995). The former approach defined the dominant loop by the relationship between one level and its net rate; the latter developed an algorithm of loop gain to find out the dominant loop with maximum loop gain. This research applied these two approaches in several models. The experiment result showed that using different approaches different dominant loops were found. For example, figure 4 is the Multiplier-Accelerator Model by Gilbert(Randers,1980), and here we focused on level Capital.

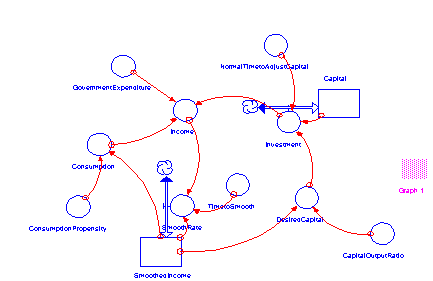
Figure 4 Multiplier-Accelerator Model (sourece:Randers, J.
Elements of the System Dynamics Method, Cambridge, Mass:M.I.T. Press, 1980)

First, we calculated the loop gain developed by Kim and found level Capital was dominated by a negative loop throughout simulation period. To probe the phenomenon, we found that there might be a problem with the algorithm of loop gain. In calculating loop gain, the algorithm isolated concurrent system variation, thus the loop gain acquired was not exactly consistent with the actual loop gain. Second, we plotted the level-rate diagram to apply Richardson's mean, the polarity of its dominant loop changed iteratively. However, from the traditional point of view, the structure diagram showed that there was only one loop around level Capital. It is an obvious example of implicit loop we referred earlier.

5. Conclusion
In this research, we focused on some concepts of dominant loop analysis methodology. First, the basic positive and negative loop behaviors were clarified more clearly. Second, nonlinearity was discussed to see if it is a necessary condition for dominant loop shift. Finally, two dominant loop analysis approaches were applied and the different analysis results were explained. From this paper, we can see that dominant loop analysis is still an undeveloped ground for researchers to explore.




References:
1.Forrester, J.W. Priciples of Systems, Cambridege, Mass:The M.I.T.Press, 1968.
2.Graham,A.K."Priciples on the Relationship Between Structures and Behavior of Dynamics Systems", Ph.D. Dissertation, M.I.T., Cambridge, 1973.
3.Kim, D.H."A New Approach for Finding Dominant Feedback Loop:Loop by Loop Simulations for Tracking Feedback Loop Gains", Proceedings of the 1995 International System Dynamics Conference, vol2, p.601-610, 1995.
4.Randers, J. Elements of the System Dynamics Method, Cambridge, Mass:M.I.T. Press, 1980.
5.Richardson, G.P., "Dominant Structure", System Dynamics Review, vol. 2, no. 1, p.68-75, 1986.
6.Richardson, G.P., "Loop Polarity, Loop Dominance, and the Concept of Dominant Polarity(1984)", System Dynamics Review, vol.11, no. 1, p.67-88, 1995.


ISDC '97 CD Sponsor