1. From Multi-Agent System (MAS) to Multi-Agent Dynamics (MAD)
Rising complexities in information transactions on networks require intelligent agents for performing economic activities for human principals. These agents are shaping an agent-space or an agent-market that is operated by distributed decision rules embedded in the individual agent. Recently a multi-agent system (MAS) represents a group of research for understanding dynamic behavior (or performances) of intelligent agent societies that reside not only in the cyberspace but also in the real world. While distributed artificial intelligence (DAI) is interested in cooperative problem solving by multiple intelligent agents, the MAS is concerned with general system behavior emerging from complex (competitive or cooperative) interactions among multiple agents.
In general, researches in the discipline of the MAS rely heavily
upon the discrete and stochastic modeling methodology, and their
analysis and predictions are devoid of insightful explanations
from the viewpoints of system structure. Furthermore, their research
methodologies are so diverse that simulation models for MAS lack
a common platform. Since system dynamics has been developed mainly
for providing direct insight on the structural mechanism of complex
systems, we believe that system dynamics is one of the most promising
methodologies for understanding multi-agent dynamics (MAD).
2. Differences between multi-agent systems and system dynamics
Recent studies on complex systems are showing deep interests in distributed and parallel mode of systems control. Both decentralization and parallel decision makings are not new to system dynamics. Both features have been inherent in system dynamics methodologies. However, while the researchers on MAS tend to focus on the individual decision makers, system dynamicists are used to conceptualizing multiple decision makers in terms of aggregated stocks and flows. Resnick points out difference between his modeling approach and that of Stella as follows.
"Both StarLog and Stella are designed to help people
explore the behaviors of systems. But there are some important
differences. In using Stella, you typically think in terms of
aggregate quantities... StarLogo, by contrast, focuses more on
individual creatures, not overall populations... The behavior
of the overall population arises out of the interactions among
the individual creatures (in StarLog)." (Resnick
1994, p.35)
The main difference between system dynamics and current researches
in MAS lies in their perspectives on the population of homogeneous
actors such as producers, transporters, and consumers (see table
1). While system dynamicists prefer to regard the population as
a single actor (a set of stock and flow variables), researchers
on multi-agent systems focus their attention on the interactions
among autonomous actors.
| 1.Unit of analysis | ||
| 2.Rationality assumption | ||
| 3.Crucial mechanism | ||
| 4.System structure | ||
| 5.Surprising value
of model | ||
| 6.Research focus |
|
|
| 7.Modeling tools | ||
| 8.Explaining tools |
|
|
| 9.Main application area | ||
| 10.Issue of learning |
|
|
3. Aggregate thinking in system dynamics modeling
Although lots of system dynamicists put an emphasis on an operational thinking, system dynamicists have used aggregation explicitly or implicitly. Aggregation provided one of the most dilemmatic choices for system dynamicists in that aggregate models sacrifice detail for simplicity.
"Aggregation is desirable and essential and yet a hazard... If there is insufficient aggregation, the model will be cluttered by unnecessary and confusing detail. If aggregation is too sweeping or accomplished by combining the wrong things, we shall lose elements of dynamic behavior that we wish to observe"(Forrester 1961, p.109).
Overuse of aggregation is detrimental not only to building correct
models, but also it keeps modelers from paying attention on interaction
mechanisms among individual elements. Aggregate thinking is prone
to ignore fundamental mechanisms at disaggregate level, such as
cooperation, competition, negotiation, auction, and trade among
individual agents. As a result, it is often the case that aggregate
model variables are too abstract and general to relate directly
to a specific decision or problem (Alfeld & Graham 1976, p.105).
4. Array variables for modeling MAS
Although MAS can be characterized by massive complexity, its complexity comes mainly from many elements rather than many relationships. Most models of MAS have simple causal structures relating many intelligent agents. This fact implies that the structural mechanism of MAS models can be represented rather succinctly by stock/flow diagram of system dynamics. Furthermore, array variables in system dynamics can be used to incorporate lots of similar agents without cluttering causal structure of MAS.
The aggregate thinking has kept system dynamicists from extensively using array variables. Stella, the most popular modeling environment in system dynamics society in these days, does not support the array variable that has been included in Dynamo. Although the array variable has been introduced mainly for simplifying a part of stock and flow diagram having similar structure, it can be also used as a tool for representing multiple agents without aggregation. In this study, we used array variables of Vensim to model multiple agents.
In general, MAS is composed not only of multiple agents but also multiple goods that are owned and traded by the former. And there are various kinds of agents who act or decide upon different causal structure. Agents and goods that have different causal structures must be represented as separate array variables.
Although Vensim and Dynamo supports array variables, there are
only basic functions for operating array variables. The most difficult
problem is that Vensim does not provide any function for permitting
direct access to one of variables contained in array variable.
(C language supports this feature by pointers, and in object oriented
programming environments one can access any elements of an array
even without particular operators.) One of the basic operations
on the array variables is to compare and choose between them.
For example, consider that a consumer must choose between product
A and B according to his utility for them. One can find what is
the maximum value of their utility with VMAX function, but he
cannot directly find what product gives the best utility. This
problem can be handled by "intermediate array variables"
that record comparison result among cells of array variables.
The intermediate array variables may contain simple binary value
(1,0) for recording an agent's decision on what products
to buy or ratio values for telling what amount of each products
to buy. Let us focus on the binary intermediate array variables.
They can be used elsewhere in the model as demonstrated in table
2. In table 2, g and c denote goods and consumers respectively.
As in table 2, one can represent most of decision variables of
multiple consumers with the intermediate array variable.
| Typical equation for BIAV ¢º biav[g,c]=IF THEN ELSE(marginal utility[g,c]=VMAX(marginal utility[g!,c]),1,0) |
| Number of best products to demand
¢º number of best product[c] = SUM(biav[g!,c]) |
| Amount of money needed for demanding unit of each best product
¢º money needed[g,c] = biav[g,c]*price[g] |
| Amount of each product to demand
¢º demand[g,c] = biav[g,c]*(SUM(money needed[g!,c])/available money[c]) |
| Total demand for each product
¢º total demand[g] = SUM(demand[g,c!]) |
5. MAS for market price system
One can find multiple agents in various kinds of social systems including organizations, teams, and markets. They can coordinate or compete each other to achieve maximal states of their respective utilities. Decision rules transform their perceived states into their intended action. Social systems as well as individual agents have their own decision rules. One can classify social systems according to what decision rules they adopt.
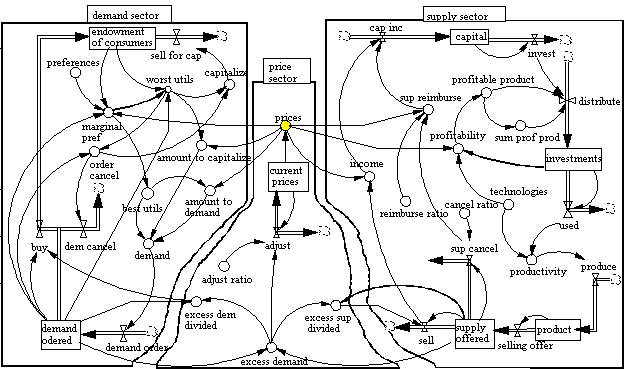
A market can be conceived as both an auction place with central auctioneer and a trading place for diverse contractors without any auctioneer. While Wellman's WALRAS environment is related with the former (Wellman 1993), the latter includes Trade Network Game (Tesfatsion 1996), StarLogo (Resnick 1995), and Contract Net Protocol (Smith 1980, Sandholm 1993). In this paper, we focused on the market as an auction place where tatonnement are proceeding to find equilibrium prices as Léon Walras pointed out in the 19th century. We chose to model a tatonnement system simply because it has more clear and fixed structure than contract net systems.
In tatonnement system, agents consisting of consumers and producers
respond to price signals for the individual goods. The agents'
interactions are coordinated by central auctioneers who adjust
the price levels to achieve a perfect balance of supply and demand.
Figure 1 demonstrates a system dynamics model for a tatonnement
system. Our model is composed of three kinds of agents: consumers,
producers, and auctioneers.

Wellman developed a WALRAS environment in which one can construct multi-agent market systems working on the process of tatonnemnt. The WALRAS system exploits the economic mechanism of general equilibrium theorem to find out efficient resource allocation in distributed and parallel manner. While WALRAS focuses on searching optimal system states, our system dynamics model is mainly for understanding complex behavior of multi-agent systems. Since our modeling purpose is descriptive rather than prescriptive, we changed two assumptions adopted in Walrasian tatonnement systems. First of all, in our model, auctioneers do not know utility functions of consumers and producers. Agents receive a price signal and report their demands and supply, and auctioneers adjusts the prices incrementally in proportion to the magnitude of excess demands. Secondly, agents are allowed to trade their goods before the economy has reached equilibrium. Economists often call these market price systems as non-tatonnement processes.
From our experience in modeling MAS, we found that system dynamics
provides a promising platform for modeling MAS. Using array variables
to represent agents, one can model MAS without cluttering the
model structure. The same stock and flow diagram displayed in
figure 1 can be used for different number of consumers, producers
and goods.
6. Simulation Results: MAD is not SAD
Although our modeling purpose is mainly for investigating possible
roles of system dynamics in the MAS research, we performed several
experiments to compare multi-agent dynamics (MAD) and single-agent
dynamics (SAD). Table 3 shows our three versions of modeling the
market price system: a single agent model (1 consumers, 2 products,
1 producers), a multi-agents model (10 consumers, 2 products,
2 producers) with identical initial endowments, and a multi-agents
model (10 consumers, 2 products, 2 producers) with different initial
endowments. Simulation results are displayed in figure 2 and figure
3.
| Average | |||
| Single Agent | product A |  | |
| product B | 
| ||
| MAS with iden-tical endowment | product A |  | |
| product B | 
| ||
| MAS with diff-rent endowment | product A | 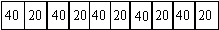 | |
| product B | 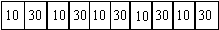
| ||
| Total endowment in price (10) | 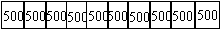 | ||
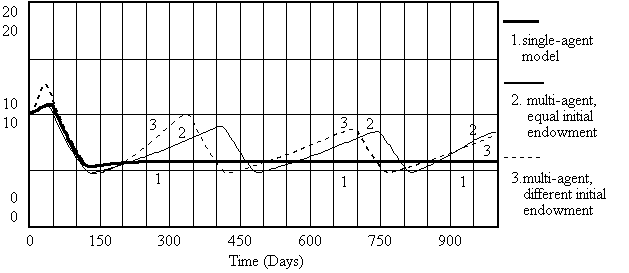 Figure 2. Price of Product 1 for
single agent model and two multi-agent models
Figure 2. Price of Product 1 for
single agent model and two multi-agent models
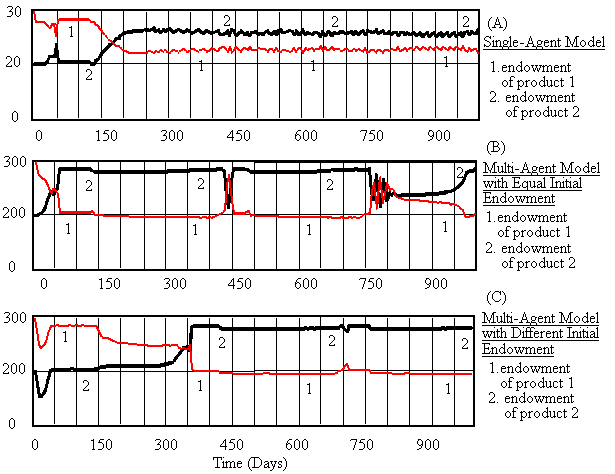
Three versions of our model are different only in the number of
consumers and producers and the consumers' initial endowments.
We maintained that consumers' average initial endowments
are same in all three versions. Although our single agent model
did not account the behavior of population, we can roughly regard
it as an aggregate model. And thus the simulation results in figure
2 and 3 cast some implications on what differences lie between
the aggregate model and multi-agent model. Figure 2 demonstrates
their differences in time behavior of price. Although single agent
model shows stabilizing tendency of the price, prices of multi-agent
models keep on fluctuating. In addition, figure 3 shows that the
endowments of consumers will change between single agent model
and multi-agent model. Furthermore figure 2 and 3 says that the
initial endowments of multi-agent model will force the system
to evolve different paths.
7. Concluding Remarks
We believe that integration of system dynamics and multi-agent systems will provide lots of insights to system dynamicists as well as researchers on MAS. System dynamicists can get more insights on the interactions effects among autonomous agents, while MAS researchers can improve their understanding into the system structures. In particular, system dynamics will provide an integrated modeling environment as well as explaining tools including causal loops and stock-flow diagrams. Furthermore, their integration will open a new way for a simulation based learning game that will permit learners taking a role of individual agents surrounded by similar agents competing or cooperating with each other.
However, their integration will require new theoretical questions.
We could not explain clearly what mechanisms produced the different
simulation results between the single-agent model and the multi-agent
model. One of the most urgent questions is how we can understand
the structural meanings of interactions among agents.
M. Resnick, 1994, Turtles, Termites, and Traffic Jams, The MIT Press.
M.P. Wellman, 1993, "A Market-Oriented Programming Environment
and its Application to Distributed Multicommodity Flow Problems,"
Journal of Artificial Intelligence Research, Vol. 1, pp.1-23.
Rising complexities in transactions on networks require intelligent agents for performing economic activities for human principals. These agents are shaping the agents-spaces or agents-markets that are operated by distributed decision rules embeded in the individual agent. Several groups of computer scientists and economists including game theorists are suggesting diverse and different approaches for simulating these multi-agents systems. However, their approaches rely heavily upon the discrete and stochastic modeling methodology, and their analysis and predictions lack insightful explanations from the viewpoints of system structure.
The main difference between system dynamics and current
researches in multi-agent systems lies in their perspectives on
the population of similar actors such as producers, transporters,
and consumers. While system dynamicists prefer to regard the population
as a single actor (a set of stock and flow variables), researchers
on multi-agent systems focus their attention on the interactions
among independent (homogenous or heterogenous) actors selected
from a few populations. In this paper, we make a system dynamics
models for the agent-based market, which can be used as an archetype
model for diverse areas of multi-agent system research. We introduce
how to model complex interactions among different actors with
array variables. Simulation results of our explorative model show
that interactions among actors from even an identical population
can produce wide range of behavioral patterns. Furthermore, we
suggest system dynamics as a modeling platform for multi-agent
system, because system dynamics model with array variables can
simplify the causal structure of complex interactions of multi-agent
systems and therefore provide many insights for policy levers.
Dr. Dong-Hwan Kim
137-070
ETRI, Techno-Economics Dept.
6th floor Leaders office Bldg. 1599-11,
Seocho-Dong, Seocho-Ku,