Production technology, in general, must internally
evolve to maturity to be fully effective in a manufacturing system.
In this article, we propose that the process of technology development
can be affected by learning occurring both inside and outside
the production system. Consistent with the model characteristics
described later, we developed a system dynamics model, based on
which we offer two significant implications: (i) an optimal dynamics
to bring initial technology from outside to inside is quite sensitive
to particular combinations of induced and autonomous learning
rates, (ii) the autonomous innovation has doubly accelerating
effects on the optimal dynamics since it affects not only
the technology costs, but also the system's induced learning
capability. For an optimal planning of technology development,
firms have to take into account the interplay between induced
and autonomous innovation.
1. Introduction
Production technology development is an essential part of operations strategy. But, production technology must become 'system-specific' to be fully effective in a manufacturing system, i.e., it must internally evolve to maturity so as to be effectively utilized. The process of technology development can be affected by innovations occurring both inside and outside the manufacturing system. Thus, the manufacturing firm must incorporate into its endogenous technology development process both internal and external innovations. A critical question is "How much initial technology needs to be brought into the internal system and when?" The question can be certainly more complicated when the rate of external innovation differs from that of internal innovation to a significant extent. In this article, we endeavor to answer the question by capitalizing on the theory and simulation of system dynamics.
There are related works in the literature. Kim (1996) suggested the importance to reach an optimal balancing between in-house technology development (i.e., internal) and outsourcing of the development efforts (i.e., external). Jaikumar and Bohn (1992) studied on "where" to create new technological knowledge, offering three such ways, (i) purchasing outside knowledge, (ii) intensive R&D outside manufacturing, and (iii) learning within existing manufacturing process. This kind of decision making was also studied under several different situations. Kennedy (1993) modeled in-house versus contract maintenance, taking into account fixed costs and learning effects. Gaimon (1985 and 1989) approached a problem of automation acquisition from a binary decision making perspective.
We view the innovation as a learning process, i.e., learning is a fundamental force for innovation (Dosi 1982). Accordingly, the difference in rates of innovation can be expressed with the learning rate difference associated with the two types of innovation. More elaborate definitions are as follows: (a) External Innovation (Autonomous Learning) is a type of learning that could occur without individual firms' conscious efforts channeled to the learning activities, i.e., autonomous, primarily correlated with a time-related variable (Adler and Clark 1991), (b) Internal Innovation (Induced Learning) is an induced learning planned and managed inside the firm, requiring intentional efforts on the managers' part (Hayes, et al. 1996).
With the model characteristics described in the next
sections, we developed a system dynamics model and ran a simulation.
The modeling details and analysis outcomes are in section 2. In
the final section, we discuss managerial implications and suggestions
for future study.
2. Analysis of a Learning Model in System Dynamics
In order to answer the research questions, we developed a system dynamics model, and ran a simulation. The model context can be described as follows: (a) in order for a production system to develop its production technology, it needs to purchase the initial technology (say, raw technology/resources) from outside, paying purchasing costs, (b) before becoming fully effective in the production process, the initial technology has to be nurtured inside the system, incurring internal nurturing costs, (c) fully nurtured technology generates profit equivalent to the unit market value, (d) autonomous innovation affects the outside purchase costs, while induced learning has an effect on the internal nurturing costs.
Assumptions related with the learning effects can be described as follows. An autonomous learning rate (ALR)=0.1, i.e., 10%, implies that as the time doubles, the unit purchase cost would be reduced by 10%. For instance, suppose ALR=0.1 and the purchase price is $10 at time 5. Then, at time 10, the purchase price will be $9, i.e., $10x(1-0.1). On the other hand, the induced learning rate (ILR) affects the internal nurturing cost, depending on the cumulative amount of technology raised inside the production system. For example, if ILR=0.1, the current nurturing cost per unit technology is $10, and the cumulative amount of technology nurtured up to date is 50 units, then the unit nurturing cost would be $9 by the time the cumulative amount reaches 100 units, i.e., doubles. This is a general learning situation, well-established in the literature (Yelle 1979).
We ran the simulation for 100 periods. Other parameters used in the simulation are defined as follows: 'initial unit purchase cost=$10, initial unit nurturing cost=$10, market value for a unit technology=$30,' and each period's technology purchase amount is determined as maximum of 5 units or 0.8x(current total profit/current unit purchase cost). Some of the limits of this particular modeling will be discussed in the last section.
Table 1. Relative Profits by Induced and Autonomous Learning Combinations I *
| |||||||||
*Base value is the value at induced learning rate=0.0 and autonomous learning rate=0.0
Table 2. Relative Profits by Induced and Autonomous Learning Combinations II **
| |||||||||
**Base value is the value at induced learning rate=0.0 for each autonomous learning rate.
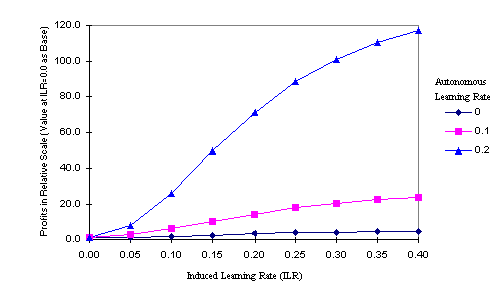
The simulation result is in Table 1 and 2. Table 1 shows the relative profits from the technology development by various combinations of induced and autonomous learning rates, its base being the profit when both induced and autonomous learning rates are zero, i.e., with no learning effects (the base value is scaled to be one, and others have scaled values relative to the base). Let's denote the profit when 'ALR=x and ILR=y' as [x, y]. Then, the base value in Table 1 is 1.0=[0.00, 0.00]. Table 2 tabulates the relative profits for each autonomous learning rate: for each autonomous learning rate, the base is the value when the autonomous learning is zero. For instance, there are three base values, [0.00, 0.00], [0.10, 0.00], and [0.20, 0.00], all scaled to be one, for the three different autonomous learning rates. The result in Table 2 is also shown in Figure 1. From this simulation analysis, we can infer:
Figure 1. Relative Profits by Induced and Autonomous Learning Combinations II
3. Implications and Discussion
In this article, we tried to investigate the dynamic effects of induced and autonomous learning on firms' production technology development. The analysis indicated that it is critical for the firms to take into account the two learning effects separately and also simultaneously when planning for technological innovation. Another implication is that the autonomous innovation can have doubly accelerating effects on the dynamics: this also implies that in order to fully capitalize on the autonomous innovation, firms must have their internal learning capability. Figure 2 suggests a dynamic cause-effect structure consistent with this analysis.
Figure 2. Dynamic Cause-Effect Relation for the Learning Model
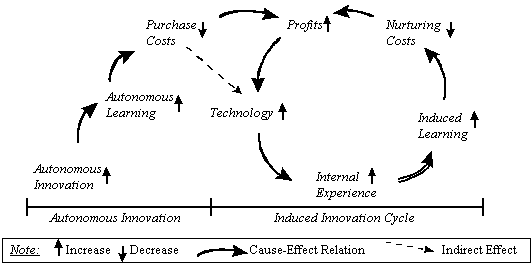
When a firm can realize strong induced learning and is operating in an environment conducive to rapid autonomous innovation, its capability to develop production technology can be greatly enhanced if it can capture the dynamic interplay between the two kinds of learning.
Although the research outcomes in this article support our propositions reasonably well, we believe it can be further improved. First, we would like to consider a more realistic setting in which a limiting or balancing mechanism plays a role: the present model does not take into account a balancing cycle that puts a limit on the amount of technology a firm can develop at a time. Second, it seems interesting to consider a situation where each different type of technology requires a different period for internal maturing. Using actual data, e.g., parameter values like purchase and nurturing costs and market value, from a particular industry should also contribute to this line of study. Finally, we would apply the model in this article to other managerial situations such as R&D and human resource management.
Adler, P. S. and Clark, K. B., 1991. Behind the learning curve: a sketch of the learning process. Management Science, 37(3): 267-281.
Dosi, G., 1982. Technological paradigms and technological trajectories. Research Policy, 11: 147-162.
Gaimon, C., 1985. The optimal acquisition of automation to enhance the productivity of labor. Management Science, 31(9): 1175-1190.
Gaimon, C., 1989. Dynamic game results of the acquisition of new technology. Operations Research, 37(3): 410-425.
Hayes, R. H., Pisano, G. P., and Upton, D. M., 1996. Strategic Operations. The Free Press.
Jaikumar, R. and Bohn, R. E., 1992. A dynamic approach to operations management: an alternative to static optimization. International Journal of Production Economics, 27: 265-282.
Kennedy, W. J., 1993. Modeling in-house vs. contract maintenance, with fixed costs and learning effects. International Journal of Production Economics, 32: 277-283.
Kim, B., 1996. Learning induced control model to allocate managerial resources for production technology development. International Journal of Production Economics, 43(2): 267-282.
Yelle, L. E., 1979. The learning curve: historical review and comprehensive study. Decision Sciences, 10: 302-328.