FUZZY LOGIC AS A METHOD FOR
THE APPLICATION OF QUALITATIVE CONCEPTS
IN A
QUANTITATIVE SYSTEM FRAMEWORK
J.L. de Kok (1), H.G. Wind(1), A.C. Coffa (1), W.L.T.
van Densen (2) and L. Pet-Soede (2)
(1) Department of Civil Engineering Technology and
Management
Twente University at Enschede, The Netherlands
(2) Department of Fish Culture and Fisheries Science
Wageningen Agricultural University at Wageningen,
The Netherlands
1. INTRODUCTION
The central aim of the ongoing research program [1] is to develop
a methodology for sustainable coastal-zone management in the tropics.
The project is based on a multidisciplinary cooperation in the
fields of economics, geography, anthropology, fisheries science,
oceanography, and marine biology. A System Dynamics approach is
followed for the management research in order to deal with the
dynamic nature of the coastal-zone processes and cross-sectoral
linkages. The integrated system model will serve to evaluate and
rank different management strategies. The disciplinary models
are based on quantitative as well as qualitative concepts. The
integration of the latter in a quantitative system framework forms
a particular problem related to integrated system modeling. In
this paper we will show how fuzzy logic may be applied to include
qualitative concepts in a quantitative simulation model .
Coral reefs are assumed to play an essential role in the abundance
and diversity of associated fish species. Data have been collected
on the structural complexity of the coral reef, the relative coverage
with living coral, and the number and species diversity of the
associated species of reef fish [2]. By means of example we will
consider the combined influence of reef complexity and live coral
coverage on the diversity of reef fish. Qualitative knowledge
on the relationship studied is stored explicitly in the form of
the fuzzy membership functions and the qualitative inference rules.
The outcomes are compared with the results obtained with a multivariate
linear regression analysis. Rather than to obtain the best possible
description of the data the intention of this paper is to show
how qualitative concepts can be incorporated in simulation models.
2. METHODOLOGY
The reef complexity is measured by underwater observations along
line transects. Depending on the degree of complexity a numerical
value within the range of 1.0 to 17.0 is assigned to the different
life forms observed, such as sand, branching coral, sponges, and
algae [2] . Sampling is based on 100 m. transects. The live coral
coverage (LCC) is defined as the ratio of line intercept to the
total length of the transect. Simultaneously, the total number
of fish and the number of fish categories are estimated. The data
set analyzed here comprises 47 sample values for the reef complexity,
the live coral coverage, and the total number of fish present
.
Prior to analysis the data are transformed to a normal distribution
according to the linear mapping 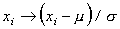 , where
and are the sample average and standard deviation respectively.
The membership function parameters are determined using the ANFIS
routine provided by the Matlab package [3], which combines a Sugeno
type fuzzy inference system with an adaptive neural backpropagation
learning algorithm [4]. For the reef complexity we use a Gaussian
type membership function
, where
and are the sample average and standard deviation respectively.
The membership function parameters are determined using the ANFIS
routine provided by the Matlab package [3], which combines a Sugeno
type fuzzy inference system with an adaptive neural backpropagation
learning algorithm [4]. For the reef complexity we use a Gaussian
type membership function 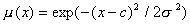 , for the LCC
we use a trapezoidal membership function:
, for the LCC
we use a trapezoidal membership function: 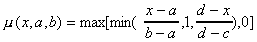 .
Consistent with linear Sugeno inference the crisp output value
for variable y is calculated directly as the linear combination
of the fuzzy values of the two numerical input variables x1 and
x2:
.
Consistent with linear Sugeno inference the crisp output value
for variable y is calculated directly as the linear combination
of the fuzzy values of the two numerical input variables x1 and
x2:
IF (x1 = "value 1") AND (x2 = "value 2")
THEN (y = p*x1 + q*x2 + r)
First the antecedent degree of membership r
is calculated for each rule r, then the numerical
output value is computed as the weighted sum over the rule antecedents
[5]:
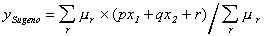
By means of example the qualitative inference rules are defined
as:
1. IF ( LCC = poor) OR (complexity = low) THEN (number fish
= low)
2. IF (LCC = fair) AND (complexity = normal) THEN (number fish
= medium)
3. IF (LCC = good) AND (complexity = high) THEN (number fish
= high)
In principle nine inference rules are possible. Thus, each
of the two input variables and the single output variable can
have three fuzzy values. The logical AND operation is performed
according to the product rule 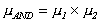 . The OR
operation is performed according to the probabilistic rule [5]
. The OR
operation is performed according to the probabilistic rule [5]
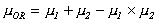 . In total 27 parameters are used by
the ANFIS routine. For comparison a multiple linear regression
analysis (MLR) was performed, using the reef complexity and live
coral coverage as independents.
. In total 27 parameters are used by
the ANFIS routine. For comparison a multiple linear regression
analysis (MLR) was performed, using the reef complexity and live
coral coverage as independents.
3. RESULTS
The ANFIS routine resulted in 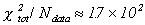 whereas
the MLR resulted in
whereas
the MLR resulted in 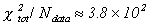 . For further comparison
the residual values for both methods are shown in Figure 1. The
membership functions obtained for the input variables with the
ANFIS routine are shown in Figure 2.
. For further comparison
the residual values for both methods are shown in Figure 1. The
membership functions obtained for the input variables with the
ANFIS routine are shown in Figure 2.
4. DISCUSSION
As expected for highly correlated input variables the ANFIS routine
performs better than the linear regression analysis. On the other
hand only three parameters are used for the linear regression,
compared to the 27 parameters for ANFIS. The main advantage of
the fuzzy approach however, is that the qualitative model concepts
are explicitly available in the form of
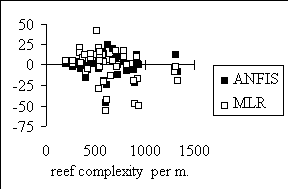
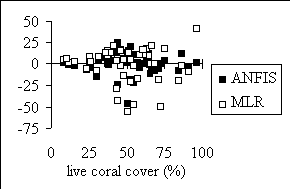
Figure 1. Residual plots for ANFIS and MLR predictions of reef
complexity and live coral cover.
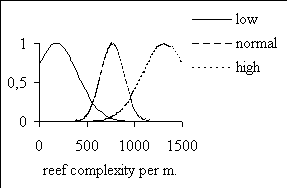
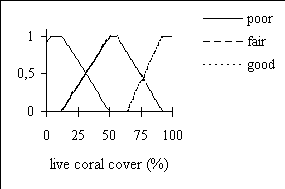
Figure 2. Membership functions obtained with ANFIS for the
reef complexity and live coral cover.
the inference rules and membership functions. As pointed out by
Tessem and Davidsen [6] fuzzy set theory may prove to be a useful
alternative for conventional methods to incorporate qualitative
concepts in simulation models, such as the table functions now
provided by simulation tools. Conditions in favor of the applying
fuzzy logic are: qualitative expert knowledge, dependency of input
variables, non-linearity of relationships, and the absence of
mathematical models.
5. REFERENCES
[1] Research program W.60.01 'Development of a methodology for
sustainable coastal-zone management in tropical countries', funded
by the Netherlands Foundation for the Advancement of Tropical
Research (WOTRO).
[2] H. van Lavieren, September, 1996. The influence of substrate
structure on coral reef fish communities in Spermonde Archipelago,
South-West Sulawesi, Indonesia, Report of a 5 months MSc thesis
in Program Buginesia Universitas Hasanuddin and WOTRO Fisheries
Project , Ujung Pandang Indonesia, , Dept. of Fish culture and
fisheries, Wageningen Agricultural University, Wageningen, The
Netherlands.
[3] Matlab Fuzzy Toolbox, 1995. The MathWorks Inc.,
[4] J.-S. R. Jang, May 1993. ANFIS: Adaptive-Network-based Fuzzy
Inference Systems, IEEE Transactions on Systems, Man, and Cybernetics,
Vol. 23, No. 3., 665-685.
[5] H.-J. Zimmermann, 1996. Fuzzy Set Theory And Its Applications,
3rd ed. Kluwer Academic Publishers.
[6] Bjrnar Tessem and Pl I. Davidsen, 1994, Fuzzy system dynamics:
an approach to vague and qualitative variables in simulation,
System Dynamics Review Vol. 10 (1), 49-62.
ISDC '97 CD Sponsor 
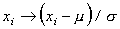 , where
and are the sample average and standard deviation respectively.
The membership function parameters are determined using the ANFIS
routine provided by the Matlab package [3], which combines a Sugeno
type fuzzy inference system with an adaptive neural backpropagation
learning algorithm [4]. For the reef complexity we use a Gaussian
type membership function
, where
and are the sample average and standard deviation respectively.
The membership function parameters are determined using the ANFIS
routine provided by the Matlab package [3], which combines a Sugeno
type fuzzy inference system with an adaptive neural backpropagation
learning algorithm [4]. For the reef complexity we use a Gaussian
type membership function 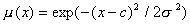 , for the LCC
we use a trapezoidal membership function:
, for the LCC
we use a trapezoidal membership function: 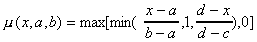 .
Consistent with linear Sugeno inference the crisp output value
for variable y is calculated directly as the linear combination
of the fuzzy values of the two numerical input variables x1 and
x2:
.
Consistent with linear Sugeno inference the crisp output value
for variable y is calculated directly as the linear combination
of the fuzzy values of the two numerical input variables x1 and
x2: 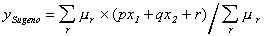
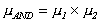 . The OR
operation is performed according to the probabilistic rule [5]
. The OR
operation is performed according to the probabilistic rule [5]
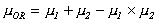 . In total 27 parameters are used by
the ANFIS routine. For comparison a multiple linear regression
analysis (MLR) was performed, using the reef complexity and live
coral coverage as independents.
. In total 27 parameters are used by
the ANFIS routine. For comparison a multiple linear regression
analysis (MLR) was performed, using the reef complexity and live
coral coverage as independents. 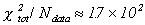 whereas
the MLR resulted in
whereas
the MLR resulted in 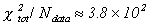 . For further comparison
the residual values for both methods are shown in Figure 1. The
membership functions obtained for the input variables with the
ANFIS routine are shown in Figure 2.
. For further comparison
the residual values for both methods are shown in Figure 1. The
membership functions obtained for the input variables with the
ANFIS routine are shown in Figure 2. 



