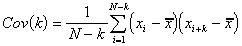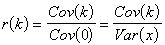
ABSTRACT

In system dynamics models, the objective of behavior validation is to check the ability of the model to generate behavior patterns similar to actual system behavior. This paper is based on a research by Barlas [1], in which he proposes a multi-step behavior validation test procedure to compare the trends, periods of oscillations, phases of oscillations, average values and amplitudes of the model and actual system behavior. The emphasis of this paper is on developing an amplitude estimation tool for oscillatory behavior patterns and a semi-automated behavior validation environment. Two approaches are utilized for the amplitude estimation procedure. First approach is based on the regression and the second one is based on Winters forecasting model for seasonal data. The behavior validation software developed, not only implements an enhanced version of Barlas's multi-step procedure but also lets the user estimate various statistical measures independently.

INTRODUCTION

In testing the behavior validity of a system dynamics model, the crucial task is to evaluate the pattern prediction ability. Thus, good models are expected to generate patterns (trends, periods, amplitudes, autocorrelations,…) that match the ones that are observed in the real data.

A multi-step behavior pattern validation procedure was proposed by Barlas [1] which lacks an effective amplitude comparison tool. The main objective of this study is to develop an amplitude comparison tool and creating a user-friendly behavior validation environment for system dynamics practitioners. The multi-step behavior validation procedure proposed by Barlas [1] includes the following six steps.

1) Trend Comparison And Removal : Trends are estimated by fitting regression curves to the outputs of the model and the actual system and the regression coefficients are compared. If the coefficients show no significant error, trend should be removed.

2) Autocorrelation Function Test For Period Comparison: Sample autocovariance and autocorrelation functions of a time series X_t is given by

for k=0,1,2,…<N.

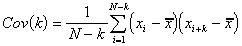
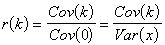
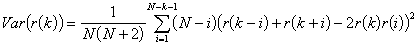
If the null-hypothesis that 'H₀: r_A(k)= r_S(k) for all k' is rejected then there exists significant errors between the periods of the model and the actual system behavior.

3) Cross-Correlation Function Test For Phase Lag Detection: The maximum of this function occurs at lag 0 if the output of the model (S) and the actual system (A) are in phase.

k=0,1..<N k=0,-1..>-N

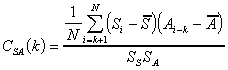
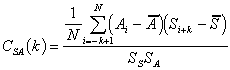
4) Comparing The Means: As a practical approach, percent error in means 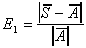can be examined to see if there is a large discrepancy between the means.

5) Comparing The (Amplitude) Variations: Percent error in the variations 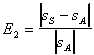can be examined to see if there is a large discrepancy between the amplitude variations. (There is a problem here, as will be seen in the next section as also mentioned in Barlas 1989 [2].)

6) Summary Measure Of Overall Behavior Discrepancy: The following discrepancy coefficient should be interpreted with great caution and rather large values should be allowed.

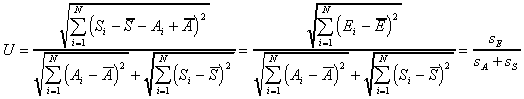
COMPARISON OF AMPLITUDES

Step 5 of Barlas's procedure is ambiguous, since it does not reveal whether a large error in E₁ is due to errors in random variations or errors in amplitudes. Thus there is a need to explicitly estimate the amplitude of S_i & A_i.

The first approach is to fit a trigonometric function to S_i & A_i , using regression. Regression approach yields a single amplitude estimate and a phase lag which defines the phase lag of the output behavior with respect to sine function. The core assumption is that sine function is a good approximation to the oscillatory behavior of the output.

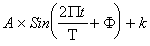
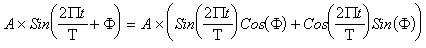
The sine function, is fitted to the output behavior where A is the amplitude, is the phase lag and k is constant. With respect to parameters A and , the regression model in question is not a linear model. In order to linearize the model, following procedure was employed.

Say U₁=ACos() and U₂=ASin(). Then the model is linear in terms of parameters U₁ and U₂. After estimating the coefficients U₁ and U₂, back transformation gives the estimation of amplitudes and phase lag.

. Hence and .

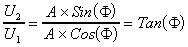
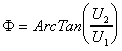
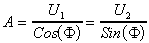
The second approach is to use a modification of Winters seasonal forecasting procedure used in forecasting literature. The underlying model is X_t=(a+bt)F_t+_t. Since the trend is assumed to be removed beforehand, b is defined to be 0 in the following discussion. The initialization process of Winters procedure is used to estimate amplitudes as described in [3].

Winters seasonal forecasting procedure works for only positive data and if any negative data exist, the minimum of the data should be subtracted from each data. The standard initialization process of Winters seasonal forecasting procedure is carried on as given in [3]. A measure of amplitude is calculated by subtracting minimum of (aNormalized F_t) from maximum of (aNormalized F_t). The proposed methodology has been suggested by Barlas and Erdem [4] but since they had negative values in their data sets, the usefulness of the procedure had been underestimated in their work.

BEHAVIOR VALIDATION ENVIRONMENT

The behavior validation environment has been developed to be used in Windows environment. Delphi is utilized in developing the environment. The environment is capable of using model output data of any simulation software, saved as text. More than simply carrying on the six step procedure developed by Barlas [1], the program can calculate various statistics independently Also for highly non-stationary, transient behavior patterns, a graphical inspection/measurement interface has been embodied into the environment.

CONCLUSION

In this paper, we first propose two amplitude estimation procedures to enhance Barlas' multi-step behavior validation procedure, and then develop a general behavior validation software. None of the amplitude estimation procedures can be said to be superior to the other, as the effectiveness of each procedure is highly case-specific. Thus the validation environment utilizes both of these procedures. The procedures proposed are only amplitude estimation procedures rather than amplitude comparison procedures. More statistical work has to be done to convert these estimation procedures into comparison procedures like estimating the standard errors of the estimates. Also proposed methodologies work for only constant amplitude cases. However they can be extended into growing or shrinking amplitude cases. The general behavior validation software developed, not only implements an enhanced version of Barlas's multi-step procedure but also lets the user estimate various statistical measures independently.

REFERENCES

[1] Barlas, Yaman; 1985; 'Validation Of System Dynamics Models With A Sequential Procedure Involving Multiple Quantitative Methods'; Ph.D. Dissertation; Georgia Institute Of Technology; Atlanta.

[2] Barlas, Yaman; 1989; 'Multiple Tests For Validation Of System Dynamics Type Of Simulation Models' ; European Journal Of Operation Research; Volume 42; 59-87.

[3] Montgomery, D.C.; Johnson, L.A.; Gardiner, J.S.; 1990; 'Forecasting And Time Series Analysis'; McGraw Hill; New York.

[4] Barlas, Yaman; Erdem, Aslý; 1994; 'Output Behavior Validation In System Dynamics Simulation'; Proceedings Of The European Simulation Symposium; Volume 1; 1-4.

ISDC '97 CD Sponsor